The Concept of the Combinatorial Mean (CMean) Conjecture
The sQuaricon Pattern and the n-Queens (p-Queens) Problem
Introduction
The n-Queens problem is well known and solved on any regular chessboard. When the problem has extended to the toroidal (modular) board it was discussed rarely in the math literature (1) and, consequently, some uncertainty occurred regarding the number of possible solutions ( e.g. oeis.A051906) on such a board. I hope, the previous enthusiastic article (2) gave some new facts regarding the ‘translated solutions’ that are kind of ostensibly solutions (see Chapter 4 in the mentioned article).
In this article, I would like to give a more concise presentation of the sQuaricon pattern matrices and go one step ahead, to present a personal hunch that we are close to some kind of the Combinatorial mean, even my hunch is fully intuitive and open to farther exploration.
Content
- the Combinatorial Grid map of natural numbers
- the sQuaricon Pattern theorem that founds an infinite sequence of the prime-number squared matrices
- the Combinatorial Mean (CMean) Conjecture as a product of the above tools. For now, it relies on sub-sQuaricon matrices as intuitive proof of the CMean existence.
- Conclusion
1. The Combinatorial Grid (CG) map of natural numbers
CG map definition:
Lets the Combinatorial Grid map be the CG(i,j) array of infinitive positive integers n, satisfying the following three conditions:

The C-Grid defines L(n) locations in the Cartesian coordinate system:

Illustration: Combinatorial Grid map of natural numbers

Pathway W(r) definition:
For n=r, let the pathway W(r) be the sequence of all r in C-Grid:

F-field is the only common element over the C-Grid map:

Small conjecture: the Combinatorial Grid map is a new prime numbers sieve
.
2. the sQuaricon Pattern theorem
Def.: The sQuaricon Pattern is an infinitive sequence of square matrices sQ(p), excerpted as modulo-p from the Combinatorial Grid map.
The sQuaricon Pattern could be constructed in two ways — manually or by modulating
2.1 Manual construction
example for p=5 in 3-steps



2.2 sQuaricon modular arithmetic design
as a modulo-p of given CMean map elements
2.2.1. sQuaricon Pattern theorem


sQuaricon Pattern theorem would have the next form:

with addendum:
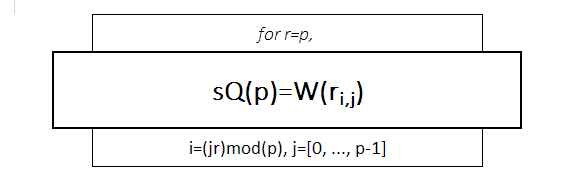
Example for sQ3:


2.2.2 F-mode vs. R-mode
An F-field has no specific value of a given r-tuple, i.e. the sQuaricon matrix is by default in F-mode.
R-mode
If we set an F-field to some specific value, then we say the sQuaricon matrix is in R-mode
2.2.3 sQuaricon matrices close up — illustration:
a) Symmetries:
sQuaricon matrix is F-centrosymmetric, while F-row and F-column symmetric elements have the same sum-p orthogonal constant (before shearing):

b) Modularity:
The sQuaricon pattern generates the modular board matrices:

Note: The number of possible solutions is discussed in (2).
c) Shear operations over the sQ matrix are not affecting the sQuaricon pattern:
- the shear-matrix operation will not change the pattern of the sQuaricon matrix,
- the F-field is the sole unmovable element in the shear operations,


The shear operation illustration:

.
3. The Combinatorial Mean Conjecture
‘In mathematics, generally, an entity is said to “exist” if a mathematical example satisfies the abstract properties that define the entity. In this sense, it may not be apparent that even a single configuration with certain specified properties exists. This situation gives rise to problems of existence and construction. There is again an important class of theorems that guarantee the existence of certain choices under appropriate hypotheses. Besides their intrinsic interest, these theorems may be used as existence theorems in various combinatorial problems.‘
3.1 The sQuaricon segments — sQ(S)
Def: the sQuaricon segments (to differentiate it from the submatrix) are repeating blocks of fields correlated to the chosen cardinal r-element on the sQ(p) modular board
3.1.1 The sQ-matrix in R-mode
To remind you, when an F-field is equal to some value of r, we say the sQuaricon matrix is in R-mode
3.1.2 The sQ-segments design in R-mode
R(r)
Let R(r) be a closed set of anchors, i.e. a set of cardinal R markers in a given sQ-matrix.
S-segment
Let S be a set of s-driftnets, i.e. a set of R-neighborhood segments that correlate to R, but never include it in the segment;
- S={s:s≠R}
- the S-segment could be of any shape and size given by R-correlative coordinates, i.e. let any R’s correlative coordinates be (0',0'), then all S’-segments have a shape given by (0'+m,0'+n)x(0'+k,0'+l).
- if m=n=-1 and k=l=1, the R will be in the center of the 3x3 S-’King’-segment.
Example:
If we explore the matrix sQ7 with R(r)=5 and S=’King’, we will get next:

Now, let’s find the correlation to s=2:

We see that s‘‘-element (as well as any other) appears 8 times (i.e. S-times) and occupies each of available 8 S-positions in the given R5-segment… i.e. any distinct vector c→s(k) appears once only.
The same pattern — S-times on all S-positions for each s≠R — repeats for any sQ matrix regardless of S-segment size and shape:
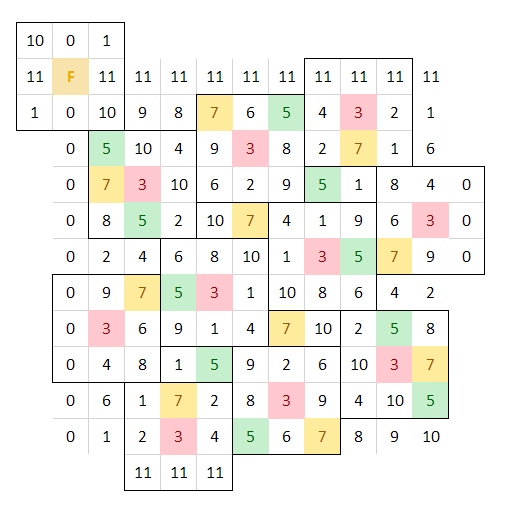

sQ19:


4. It’s too early to make any conclusion
The question is ‘what the Combinatorial Mean should be?’, does it exist, and then (if yes) is it possible to search for a math definition?
.
Note:
I am a long-time enthusiast in math and would like to keep this status in future. So, all my claims exposed here should be taken with reasonable caution at least until the full experts’ verification. This article is a preprint version in work…
